Skip to main content
Mechanical Engineering
Johnson Group

Research

Grain Boundary Structure-Property Model Development

Structure-Property Model for H Diffusivity in [100] Tilt GBs in Ni at 700 K
Reprinted from Acta Materialia, 215, Johnson, et al., Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni, 116967, Copyright 2021, with permission from Elsevier.
Structure-Property Model for H Diffusivity in [100] Tilt GBs in Ni at 700 K
Reprinted from Acta Materialia, 215, Johnson, et al., Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni, 116967, Copyright 2021, with permission from Elsevier.

We employ Bayesian inference techniques to develop structure-property models for grain boundaries (GBs) including self-diffusion, interstitial hydrogen diffusion, GB energy, etc. We develop methods that guarantee that such structure-property models respect necessary crystallographic symmetries and other physical constraints.

  • Baird, Homer, Fullwood, Johnson, “Five degree-of-freedom property interpolation of arbitrary grain boundaries via Voronoi fundamental zone framework,” Computational Materials Science, vol. 200, 110756 (2021). doi: 10.1016/j.commatsci.2021.110756
  • Johnson, Homer, Fullwood, Page, Varela, Baird, “Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni,” Acta Materialia, vol. 215, 116967 (2021). doi: 10.1016/j.actamat.2021.116967
  • Snow, Baird, Kurniawan, Fullwood, Homer, Johnson, “Grain boundary structure-property model inference using polycrystals: The underdetermined case,” Acta Materialia, vol. 209, 116769 (2021). doi: 10.1016/j.actamat.2021.116769
  • Kurniawan, Baird, Fullwood, Homer, Johnson, “Grain boundary structure–property model inference using polycrystals: the overdetermined case,” Journal of Materials Science, 55(4), pp. 1562–1576 (2020). doi: 10.1007/s10853-019-04125-z

Bayesian Inference & Uncertainty Quantification

Image of uncertainty propagation process for mesoscale simulations.
Reprinted from Acta Materialia, 215, Johnson, et al., Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni, 116967, Copyright 2021, with permission from Elsevier.
Image of uncertainty propagation process for mesoscale simulations.
Reprinted from Acta Materialia, 215, Johnson, et al., Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni, 116967, Copyright 2021, with permission from Elsevier.

We employ Bayesian techniques to do uncertainty quantification (UQ) for GB property measurements/calculations. This UQ is then incorporated into Bayesian inference strategies for the development of probabilistic GB structure-property models. We then incorporate these probabilistic constitutive models into mesoscale simulations and perform uncertainty propagation to predict the effective properties of polycrystals with rigorous UQ.

  • Baird, Homer, Fullwood, Johnson, “Five degree-of-freedom property interpolation of arbitrary grain boundaries via Voronoi fundamental zone framework,” Computational Materials Science, vol. 200, 110756 (2021). doi: 10.1016/j.commatsci.2021.110756
  • Johnson, Homer, Fullwood, Page, Varela, Baird, “Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni,” Acta Materialia, vol. 215, 116967 (2021). doi: 10.1016/j.actamat.2021.116967
  • Snow, Baird, Kurniawan, Fullwood, Homer, Johnson, “Grain boundary structure-property model inference using polycrystals: The underdetermined case,” Acta Materialia, vol. 209, 116769 (2021). doi: 10.1016/j.actamat.2021.116769
  • Kurniawan, Baird, Fullwood, Homer, Johnson, “Grain boundary structure–property model inference using polycrystals: the overdetermined case,” Journal of Materials Science, 55(4), pp. 1562–1576 (2020). doi: 10.1007/s10853-019-04125-z

Property Localization

Image of a bicrystal and a polycrystal to illustrate how one can learn a large amount about a single grain boundary with bicrystals vs. a small amount about many grain boundaries with polycrystals.
Adapted from Acta Materialia, 209, Snow et al., Grain boundary structure-property model inference using polycrystals: The underdetermined case, 116769, Copyright (2021), with permission from Elsevier.
Image of a bicrystal and a polycrystal to illustrate how one can learn a large amount about a single grain boundary with bicrystals vs. a small amount about many grain boundaries with polycrystals.
Adapted from Acta Materialia, 209, Snow et al., Grain boundary structure-property model inference using polycrystals: The underdetermined case, 116769, Copyright (2021), with permission from Elsevier.

Bicrystals permit interrogation of the properties of individual grain boundaries (GBs) directly, but can be difficult, time-intensive, or expensive to synthesize experimentally. In contrast, polycrystals are ubiquitous, contain a broad diversity of GB types, and can be more straightforward and inexpensive to produce. We have developed a Bayesian inference strategy designed to enable the use of homogenized effective property measurements from polycrystals for the construction of grain boundary structure-property models. This strategy involves the solution of an inverse problem (determining the properties of individual GBs from the homogenized properties of polycrystals) and naturally provides uncertainty quantification (UQ) for the resulting GB structure-property models. We find that under certain circumstances bicrystal data is preferred, while under other circumstances the use of polycrystal data may be more advantageous. It is likely that the optimal solution involves a combination of both types of data.

  • Snow, Baird, Kurniawan, Fullwood, Homer, Johnson, “Grain boundary structure-property model inference using polycrystals: The underdetermined case,” Acta Materialia, vol. 209, 116769 (2021). doi: 10.1016/j.actamat.2021.116769
  • Kurniawan, Baird, Fullwood, Homer, Johnson, “Grain boundary structure–property model inference using polycrystals: the overdetermined case,” Journal of Materials Science, 55(4), pp. 1562–1576 (2020). doi: 10.1007/s10853-019-04125-z

Property Homogenization

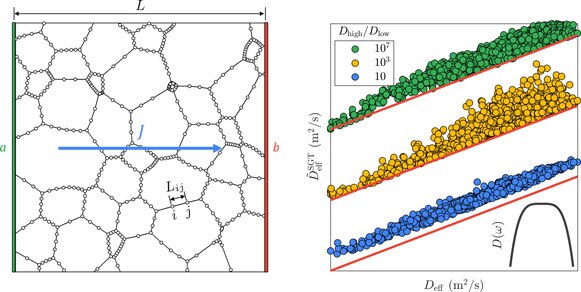
Image of a grain boundary network and a plot of the predicted vs exact effective diffusivity of the grain boundary network.
Adapted from Acta Materialia, 146, Johnson, et al., Spectral graph theory for characterization and homogenization of grain boundary networks, pp. 42-54, Copyright 2018, with permission from Elsevier.
Image of a grain boundary network and a plot of the predicted vs exact effective diffusivity of the grain boundary network.
Adapted from Acta Materialia, 146, Johnson, et al., Spectral graph theory for characterization and homogenization of grain boundary networks, pp. 42-54, Copyright 2018, with permission from Elsevier.

We develop methods to predict the effective properties of polycrystals from a knowledge of the microstructure and an underlying grain boundary structure-property model. We employ a variety of tools including spectral graph theory.

  • Johnson, Lund, Critchfield, “Spectral Graph Theory for Characterization and Homogenization of Grain Boundary Networks,” Acta Materialia. vol. 146, March, pp. 42-54 (2018). doi: 10.1016/j.actamat.2017.11.054
  • Snow, Baird, Kurniawan, Fullwood, Homer, Johnson, “Grain boundary structure-property model inference using polycrystals: The underdetermined case,” Acta Materialia, vol. 209, 116769 (2021). doi: 10.1016/j.actamat.2021.116769
  • Kurniawan, Baird, Fullwood, Homer, Johnson, “Grain boundary structure–property model inference using polycrystals: the overdetermined case,” Journal of Materials Science, 55(4), pp. 1562–1576 (2020). doi: 10.1007/s10853-019-04125-z

Microstruture Design

1 of 5
GameImage1.jpg
2 of 5
GameImage2.jpg
3 of 5
GameImage3.jpg
4 of 5
Humans-vs-SA.jpg
Human players outperform global optimization (simulated annealing) in both solution quality and efficiency for a microstructure design problem.
5 of 5
HierarchicalSimplexSampling.jpg
Reprinted from Acta Materialia, 147, Johnson, et al., An efficient algorithm for generating diverse microstructure sets and delineating properties closures, pp. 313-321, Copyright 2018, with permission from Elsevier.
1 of 5
1 of 5
GameImage1.jpg
2 of 5
GameImage2.jpg
3 of 5
GameImage3.jpg
4 of 5
Humans-vs-SA.jpg
Human players outperform global optimization (simulated annealing) in both solution quality and efficiency for a microstructure design problem.
5 of 5
HierarchicalSimplexSampling.jpg
Reprinted from Acta Materialia, 147, Johnson, et al., An efficient algorithm for generating diverse microstructure sets and delineating properties closures, pp. 313-321, Copyright 2018, with permission from Elsevier.
1 of 5

We develop and employ a variety of theoretical and computational techniques to design microstructures with optimized/tailored properties, with an emphasis on macroscopic properties that are strongly influenced by grain boundaries. These include traditional tools like microstructure hulls, property closures, spectral decomposition, and Monte Carlo techniques, as well as novel approaches like crowdsourcing and gamification as shown in the image above, which is a screen shot from a microstructure design video game developed in our group and available for public download on STEAM (https://store.steampowered.com/app/2053100/Operation_Forge_the_Deep/).

  • Adair, Evans, Beatty, Hansen, Holladay, Johnson, "Microstructure Design Using a Human Computation Game", Materialia, 101544 (2022). doi: 10.1016/j.mtla.2022.101544
  • Johnson, Kurniawan, “An Efficient Algorithm for Generating Diverse Microstructure Sets and Delineating Properties Closures,” Acta Materialia. vol. 147, April, pp. 313-321 (2018). doi: 10.1016/j.actamat.2018.01.004
  • Johnson, Schuh, “Texture Mediated Grain Boundary Network Design in Three Dimensions,” Mechanics of Materials. vol. 118, March, pp. 94-105 (2018). doi: 10.1016/j.mechmat.2017.12.001
  • Johnson, Schuh, “The Triple Junction Hull: Tools for Grain Boundary Network Design,” Journal of the Mechanics and Physics of Solids, vol. 69, no. 1, pp. 2-13 (2014). doi: 10.1016/j.jmps.2014.04.005
  • Johnson, Schuh, “The uncorrelated triple junction distribution function: Towards grain boundary network design,” Acta Materialia, vol. 61, no. 8, pp. 2863–2873, (2013). doi: 10.1016/j.actamat.2013.01.025

Grain Boundary Kinetics (Diffusion, Mobility, Grain Growth)

Eigenspectrum during grain growth with microstructures from initial and final time step.
Eigenspectrum during grain growth with microstructures from initial and final time step.

We study a variety of kinetic properties of individual grain boundaries and grain boundary networks including self- and interstitial-diffusion, grain boundary mobility, and grain growth. We investigate the influence of anisotropy, grain boundary character, and applied forces on the kinetic behavior of grain boundaries.

  • Niño, Johnson, “Influence of Grain Boundary Energy Anisotropy on the Evolution of Grain Boundary Network Structure during 3D Anisotropic Grain Growth,” Computational Materials Science, vol. 217, 111879 (2023). doi: 10.1016/j.commatsci.2022.111879
  • Homer, Johnson, Britton, Patterson, Sevy, Thompson, “A classical equation that accounts for observations of non-Arrhenius and cryogenic grain boundary migration,” npj Computational Materials, vol. 8, 157 (2022). doi: 10.1038/s41524-022-00835-2
  • Johnson, Homer, Fullwood, Page, Varela, Baird, “Inference and uncertainty propagation of GB structure-property models: H diffusivity in [100] tilt GBs in Ni,” Acta Materialia, vol. 215, 116967 (2021). doi: 10.1016/j.actamat.2021.116967
  • Snow, Baird, Kurniawan, Fullwood, Homer, Johnson, “Grain boundary structure-property model inference using polycrystals: The underdetermined case,” Acta Materialia, vol. 209, 116769 (2021). doi: 10.1016/j.actamat.2021.116769
  • Kurniawan, Baird, Fullwood, Homer, Johnson, “Grain boundary structure–property model inference using polycrystals: the overdetermined case,” Journal of Materials Science, 55(4), pp. 1562–1576 (2020). doi: 10.1007/s10853-019-04125-z

Characterization of Grain Boundaries and Grain Boundary Networks

Plot of two grain boundary networks colored by their diffusivity weighted eigenvectors.
Adapted from Acta Materialia, 146, Johnson, et al., Spectral graph theory for characterization and homogenization of grain boundary networks, pp. 42-54, Copyright 2018, with permission from Elsevier.
Plot of two grain boundary networks colored by their diffusivity weighted eigenvectors.
Adapted from Acta Materialia, 146, Johnson, et al., Spectral graph theory for characterization and homogenization of grain boundary networks, pp. 42-54, Copyright 2018, with permission from Elsevier.

Developing structure-property models for grain boundaries and grain boundary networks requires an understanding of their atomic, crystallographic, and topological structure. We employ and develop a variety of experimental and computational techniques to characterize the structure of grain boundaries at various length-scales including electron microscopy (e.g. EBSD), stereology, spectral graph theory, common neighbor analysis, and others.

  • Critchfield, Johnson, “Representative and Statistical Volume Elements for Grain Boundary Networks: A Stereological Approach,” Acta Materialia, vol. 188, pp. 166-180 (2020). doi: 10.1016/j.actamat.2019.12.029
  • Snow, Doty, Johnson, “A Simple Approach to Atomic Structure Characterization for Machine Learning of Grain Boundary Structure-Property Models,” Frontiers in Materials, vol. 6, May, pp. 120 (2019). doi: 10.3389/fmats.2019.00120
  • Johnson, Lund, Critchfield, “Spectral Graph Theory for Characterization and Homogenization of Grain Boundary Networks,” Acta Materialia. vol. 146, March, pp. 42-54 (2018). doi: 10.1016/j.actamat.2017.11.054